Gravitational Lensing by Spinning Black Holes

It showed portions of the accretion disk swinging up over the top and down under Gargantua's shadow, and also in front of the shadow's equator, producing an image of a split shadow that has become iconic for the movie.

This weird distortion of the glowing disk was caused by gravitational lensing--a process by which light beams from different parts of the disk, or from distant stars, are bent and distorted by the black hole, before they arrive at the movie's simulated camera.

This lensing happens because the black hole creates an extremely strong gravitational field, literally bending the fabric of spacetime around itself, like a bowling ball lying on a stretched out bed sheet.

The mapping of the camera's local sky (θcs,ϕcs) onto the celestial sphere (θ′,ϕ′) via a backward directed light ray; and the evolution of a ray bundle, that is circular at the camera, backward along the ray to its origin, an ellipse on the celestial sphere.

Gravitational lensing of a star field by a nonspinning black hole, as seen by a camera in a circular geodesic orbit at radius r=30M. Picture courtesy Alain Riazuelo, from his film clip \cite{Riazuelo14}; coloured markings by us.

 Light rays around a Schwarzschild Black hole: geometric construction for explaining Figure

Gravitational lensing of a star field by a black hole with spin parameter a/M=0.999, as seen by a camera in a circular, equatorial geodesic orbit at radius rc=6.03M. The red curves are the trajectories of primary images, on the camera's sky, for stars at celestial-sphere latitudes θ′=0.13π,0.26π,0.40π,0.60π,0.74π,0.87π. The yellow curves are the trajectories of secondary images for stars at θ′=0.35π,0.65π. The picture in this figure is a still from our first film clip archived at \cite{DnegSite} and is copyright \copyright 2015 Warner Bros. Entertainment Inc. INTERSTELLAR and all related characters and elements are trademarks of and \copyright Warner Bros. Entertainment Inc. (s15). The full figure appears in the second and later printings of \cite{TSI}.

The primary and secondary caustics on the celestial sphere, for the past light cone of a camera moving along a circular, equatorial, geodesic orbit at radius rc=6.03M around a black hole with spin parameter a=0.999M. As the camera moves, in the camera's reference frame a star at θ′=0.608π travels along the dashed-line path.

Two stills from a film clip at \cite{DnegSite}). In the left still, images 2 and 3 have just been created as their star passed through caustic point A of Figure ???a. In the right still, images 1 and 2 are about to annihilate as their star passes through caustic point B.

The tracks on the camera sky traveled by the multiple images of a single star, as the camera travels once around a black hole with a/M=0.999. The camera's orbit is a circular, equatorial geodesic with radius rc=6.03M. (a) For a star at latitude θ′=0.60π (18o above the equatorial plane; essentially the same star as in Figure ???a). (b) For a star at θ′=0.51π (1.8o above the equator). The tracks are labeled by the order of their stellar images (the number of poloidal, θ, turning points on the ray that brings an image to the camera).

(a) Black-hole shadow and three critical curves for a camera traveling on a circular, geodesic, equatorial orbit at radius rc=2.60M in the equatorial plane of a black hole that has spin a/M=0.999. (b) Blowup of the equatorial region near the shadow's flat left edge. The imaged star field is adapted from the Tycho-2 catalogue \cite{Tycho2} of the brightest 2.5 million stars seen from Earth, so it shows multiple images of the galactic plane.


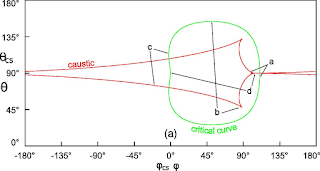
(a) The secondary caustic (red) on the celestial sphere and secondary critical curve (green) on the camera's sky, for the black hole and camera of Figure ???. Points on each curve that are ray-mapped images of each other are marked by letters a, b, c, d. (b) The tertiary caustic and tertiary critical curve.



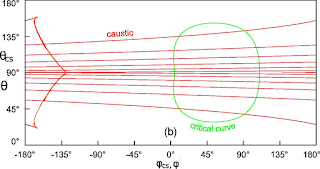
(a) The secondary caustic (red) on the celestial sphere and secondary critical curve (green) on the camera's sky, for the black hole and camera of Figure ???. Points on each curve that are ray-mapped images of each other are marked by letters a, b, c, d. (b) The tertiary caustic and tertiary critical curve

 (a) The secondary caustic (red) on the celestial sphere and secondary critical curve (green) on the camera's sky, for the black hole and camera of Figure ???. Points on each curve that are ray-mapped images of each other are marked by letters a, b, c, d. (b) The tertiary caustic and tertiary critical curve

(a) A checkerboard pattern of paint swatches placed on the celestial sphere of a black hole

with spin a/M=0.999. As the camera, moves around a circular, equatorial, geodesic orbit at radius rc=2.60M, stars move along horizontal dashed lines relative to the camera. (b) This checkerboard pattern as seen gravitationally lensed on the camera's sky. Stellar images move along the dashed curves. The primary and secondary critical curves are labeled ``1CC" and ``2CC". (c) Blowup of the camera's sky near the left edge of the hole's shadow; ``3CC" is the tertiary critical curve.

(a) A checkerboard pattern of paint swatches placed on the celestial sphere of a black hole with spin a/M=0.999. As the camera, moves around a circular, equatorial, geodesic orbit at radius rc=2.60M, stars move along horizontal dashed lines relative to the camera. (b) This checkerboard pattern as seen gravitationally lensed on the camera's sky. Stellar images move along the dashed curves. The primary and secondary critical curves are labeled ``1CC" and ``2CC". (c) Blowup of the camera's sky near the left edge of the hole's shadow; ``3CC" is the tertiary critical curve.

 Influence of aberration, due to camera motion, on gravitational lensing by a black hole with a/M=0.999. The celestial sphere is covered by the paint-swatch checkerboard of Figure ???a, the camera is at radius rc=2.60M and is moving in the azimuthal \mbeϕ^ direction, and the camera speed is: (a) that of a prograde, geodesic, circular orbit (same as Figure ???b), (b) that of a zero-angular-momentum observer (a FIDO), and (c) at rest in the Boyer-Lindquist coordinate system. The coordinates are the same as in Figure ???b.

 Influence of aberration, due to camera motion, on gravitational lensing by a black hole with a/M=0.999. The celestial sphere is covered by the paint-swatch checkerboard of Figure ???a, the camera is at radius rc=2.60M and is moving in the azimuthal \mbeϕ^ direction, and the camera speed is: (a) that of a prograde, geodesic, circular orbit (same as Figure ???b), (b) that of a zero-angular-momentum observer (a FIDO), and (c) at rest in the Boyer-Lindquist coordinate system. The coordinates are the same as in Figure ???b.

 Influence of aberration, due to camera motion, on gravitational lensing by a black hole with a/M=0.999. The celestial sphere is covered by the paint-swatch checkerboard of Figure ???a, the camera is at radius rc=2.60M and is moving in the azimuthal \mbeϕ^ direction, and the camera speed is: (a) that of a prograde, geodesic, circular orbit (same as Figure ???b), (b) that of a zero-angular-momentum observer (a FIDO), and (c) at rest in the Boyer-Lindquist coordinate system. The coordinates are the same as in Figure ???b.

Inset: Paint-swatch accretion disk with inner and outer radii r=9.26M and r=18.70M before being placed around a black hole. Body: This paint-swatch disk, now in the equatorial plane around a black hole with a/M=0.999, as viewed by a camera at rc=74.1M and θc=1.511 (86.56o), ignoring frequency shifts, associated colour and brightness changes, and lens flare. [Figure from \emph{The Science of Interstellar} \cite{TSI}, created by our Double Negative team, and TM \& \copyright Warner Bros. Entertainment Inc. (s15)]

A moderately realistic accretion disk, created by Double Negative artists and gravitationally lensed by the same black hole with a/M=0.999 as in Figure ??? and with the same geometry.

(a) The moderately realistic accretion disk of Figure ??? but with the black hole's spin slowed from a/M=0.999 to a/M=0.6 for reasons discussed in the text. (b) This same disk with its colours (light frequencies ν) Doppler shifted and gravitationally shifted. (c) The same disk with its specific intensity (brightness) also shifted in accord with Liouville's theorem, Iν∝ν3. This image is what the disk would truly look like to an observer near the black hole.

(a) The moderately realistic accretion disk of Figure ??? but with the black hole's spin slowed from a/M=0.999 to a/M=0.6 for reasons discussed in the text. (b) This same disk with its colours (light frequencies ν) Doppler shifted and gravitationally shifted. (c) The same disk with its specific intensity (brightness) also shifted in accord with Liouville's theorem, Iν∝ν3. This image is what the disk would truly look like to an observer near the black hole.

(a) The moderately realistic accretion disk of Figure ??? but with the black hole's spin slowed from a/M=0.999 to a/M=0.6 for reasons discussed in the text. (b) This same disk with its colours (light frequencies ν) Doppler shifted and gravitationally shifted. (c) The same disk with its specific intensity (brightness) also shifted in accord with Liouville's theorem, Iν∝ν3. This image is what the disk would truly look like to an observer near the black hole.

The accretion disk of Figure ???a (no colour or brightness shifts) with lens flare added---a type of lens flare called ``veiling flare'', which has the look of a soft glow and is very characteristic of IMAX camera lenses. This is a variant of the accretion disk seen in \emph{Interstellar}. [Figure created by our Double Negative team using DNGR, and TM \& \copyright Warner Bros. Entertainment Inc. (s15)]

Left-to-right: No motion blur; Monte Carlo motion blur with four time samples per-pixel; Analytic motion blur. Relative computation time is approximately in the ratio 1:4:2. Lens flare has been added to each image to illustrate how these images would typically be seen in the context of a movie.

Source: http://inspirehep.net